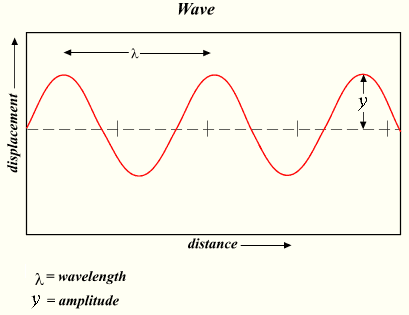
COMO RESOLVER EJERCICIOS DE ONDAS
1. La velocidad de una onda es 20 m/seg y la frecuencia es de 100 hertz. ¿Cuál es la longitud de la onda?
Solución:

2. La distancia entre dos puntos consecutivos de una onda que vibra en forma identica es 2 m. Si la frecuencia es de 10 Hertz. ¿Cuál es la velocidadde propagación de la onda?

3. El Periódo de una onda es de 0,75 seg y su lomgitud es de 1,50 m. ¿Cuál es la velocidad de propagación?


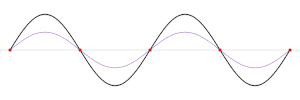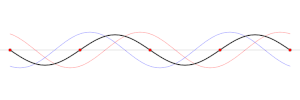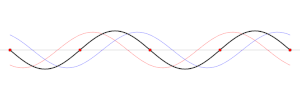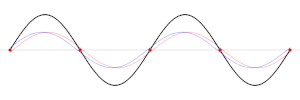
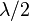

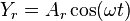 donde
donde 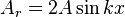
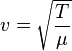






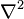 es el
es el 

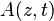 es la amplitud de la onda,
es la amplitud de la onda,  es el número de onda y
es el número de onda y  es la
es la