Ecuación de onda
La ecuación de onda es un tipo de ecuación diferencial que describe la evolución de una onda armónica simple a lo largo del tiempo. Esta ecuación presenta ligeras variantes dependiendo de como se transmite la onda, y del medio a través del cual se propaga. Si consideramos una onda unidimensional que se transmite a lo largo de una cuerda en el eje x, a una velocidad  y con una amplitud
y con una amplitud  (que generalmente depende tanto de
(que generalmente depende tanto de  y de
y de  ), la ecuación de onda es:
), la ecuación de onda es:
 y con una amplitud
y con una amplitud  (que generalmente depende tanto de
(que generalmente depende tanto de  y de
y de  ), la ecuación de onda es:
), la ecuación de onda es:
Trasladado a tres dimensiones, sería
donde 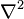 es el operador laplaciano.
es el operador laplaciano.
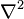 es el operador laplaciano.
es el operador laplaciano.
La velocidad  depende del tipo de onda y del medio a través del cual viaja.
depende del tipo de onda y del medio a través del cual viaja.
 depende del tipo de onda y del medio a través del cual viaja.
depende del tipo de onda y del medio a través del cual viaja.Onda simple
es una perturbación que varía tanto con el tiempo  como con la distancia
como con la distancia  de la siguiente manera:
de la siguiente manera:
 como con la distancia
como con la distancia  de la siguiente manera:
de la siguiente manera:
donde 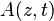 es la amplitud de la onda,
es la amplitud de la onda,  es el número de onda y
es el número de onda y  es la fase. La velocidad de fase vf de esta onda está dada por
es la fase. La velocidad de fase vf de esta onda está dada por
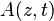 es la amplitud de la onda,
es la amplitud de la onda,  es el número de onda y
es el número de onda y  es la fase. La velocidad de fase vf de esta onda está dada por
es la fase. La velocidad de fase vf de esta onda está dada por
donde  es la longitud de onda.
es la longitud de onda.
 es la longitud de onda.
es la longitud de onda.


No hay comentarios.:
Publicar un comentario